Steps for NeutralX
01
Expanding Datasets to Prevent Overfitting
Collect data to ensure the dataset is large enough, as a small dataset can lead to the risk
of
overfitting (where a model performs well on training samples but poorly on the test
set).Common
solutions include applying random rotations, translations, cropping, altering image
brightness,
sharpness, contrast, or adding noise to the images, all of which can help expand the
dataset.
learn more
02
Expanding Datasets to Prevent Overfitting
Divide the dataset into training and testing sets. The training set is used to optimize the
model's performance and internal parameters, while the testing set is for evaluating the
model's performance. Typically, the ratio of the training set to the testing set is 70:30 or
80:20. If the dataset is large enough, even extracting 1% or 0.1% can yield thousands of
samples, allowing for more data to be allocated to the training set for performance
optimization.
learn more
03
Expanding Datasets to Prevent Overfitting
Collect data to ensure the dataset is large enough, as a small dataset can lead to the risk
of
overfitting (where a model performs well on training samples but poorly on the test
set).Common
solutions include applying random rotations, translations, cropping, altering image
brightness,
sharpness, contrast, or adding noise to the images, all of which can help expand the
dataset.
learn more
04
Expanding Datasets to Prevent Overfitting
Collect data to ensure the dataset is large enough, as a small dataset can lead to the risk
of
overfitting (where a model performs well on training samples but poorly on the test
set).Common
solutions include applying random rotations, translations, cropping, altering image
brightness,
sharpness, contrast, or adding noise to the images, all of which can help expand the
dataset.
learn more
05
Expanding Datasets to Prevent Overfitting
Collect data to ensure the dataset is large enough, as a small dataset can lead to the risk
of
overfitting (where a model performs well on training samples but poorly on the test
set).Common
solutions include applying random rotations, translations, cropping, altering image
brightness,
sharpness, contrast, or adding noise to the images, all of which can help expand the
dataset.
learn more
06
Expanding Datasets to Prevent Overfitting
Collect data to ensure the dataset is large enough, as a small dataset can lead to the risk
of
overfitting (where a model performs well on training samples but poorly on the test
set).Common
solutions include applying random rotations, translations, cropping, altering image
brightness,
sharpness, contrast, or adding noise to the images, all of which can help expand the
dataset.
learn more
Overview of NeutralX
Neuron Structure
Feedforward
Example
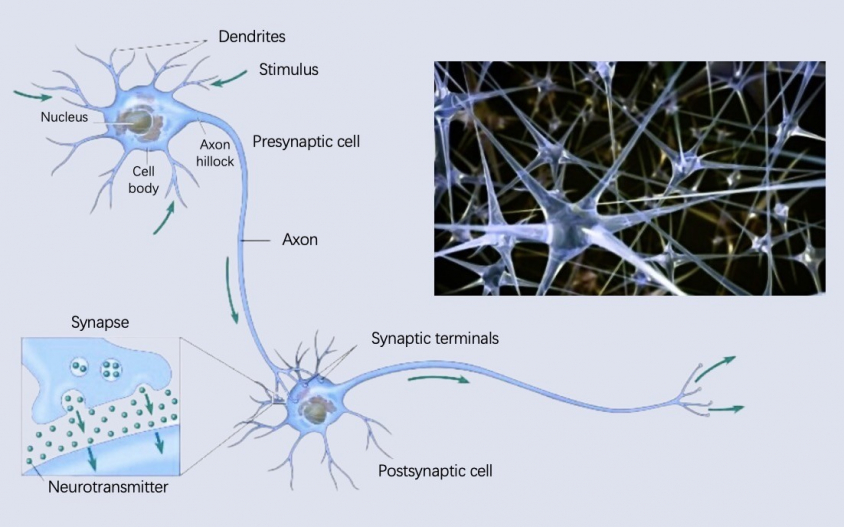
Description
Neural networks are composed of interconnected units known as neurons. Each neuron
functions
similarly to a logistic regression function, equipped with its own weights and biases,
which
serve as the model's parameters. The connections among neurons can vary, creating
diverse
neural network architectures, all of which are designed manually.
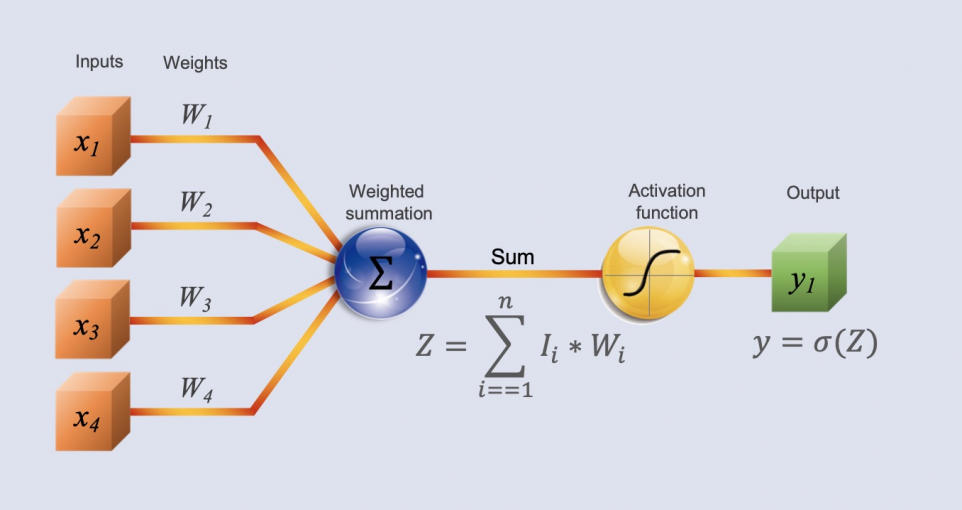
Neuron Structure
We multiply each input by its corresponding weight, sum the results, and obtain
Z;Substitute and into the activation function to obtain the result y.
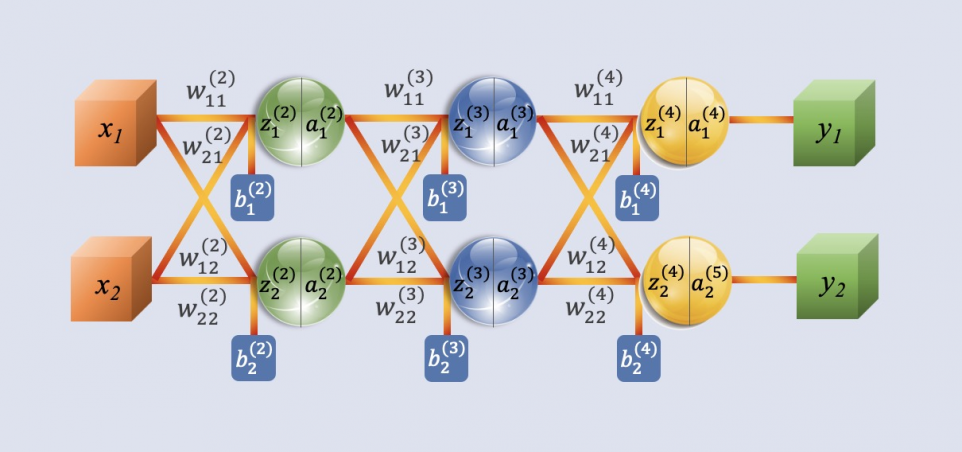
Feedforward Neural Networks
A feedforward neural network is characterized by unidirectional signal flow, meaning
that input signals move from the input layer to the output layer without feedback
connections between any two layers.
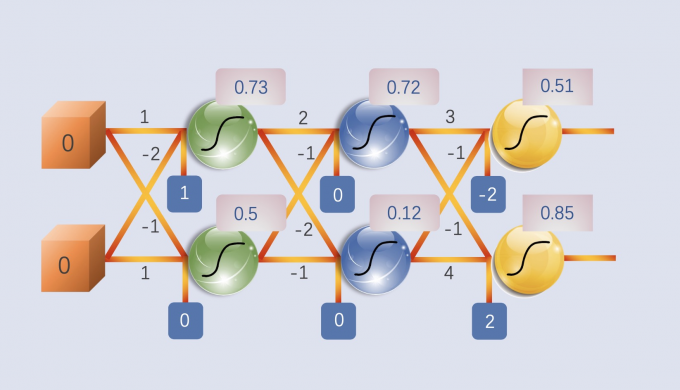
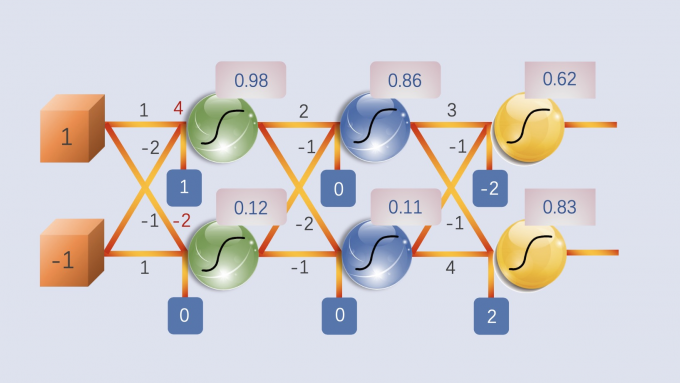
The network input is (1, -1), with the activation function being sigmoid, returning
the results as shown in the figure.
The network input is (0, 0), with the activation function being sigmoid, returning
the results as shown in the figure.
WRITE PRODUCT REVIEW
Model Evaluation
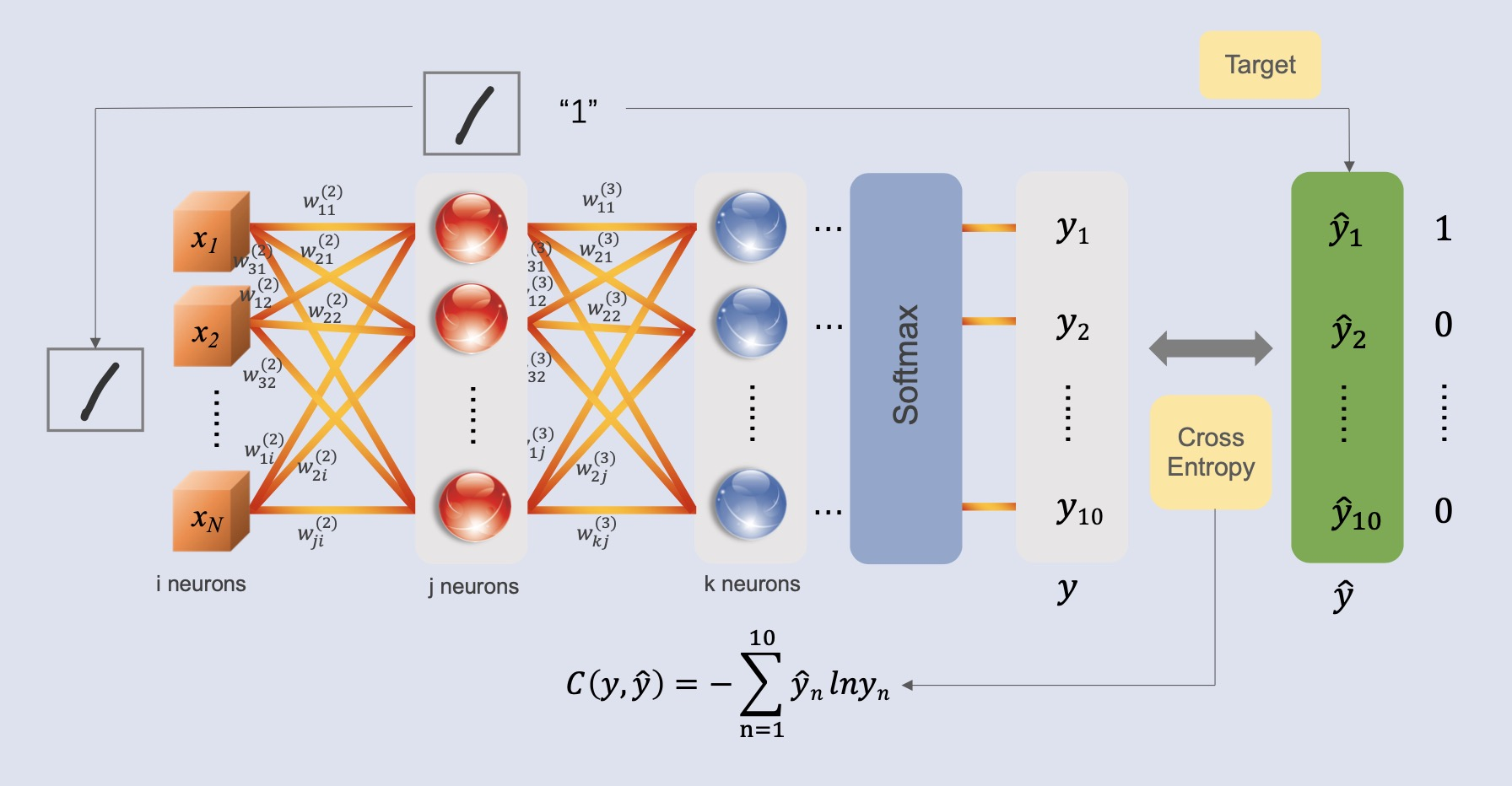
Optimizing Model Performance
To evaluate a model, we typically use a loss function to reflect its performance. For neural
networks, the cross-entropy loss function is commonly employed to measure the loss between
predicted and true labels. Our objective is to minimize this cross-entropy loss by adjusting
the
parameters of the model, aiming for a lower loss value to improve model performance.
learn more
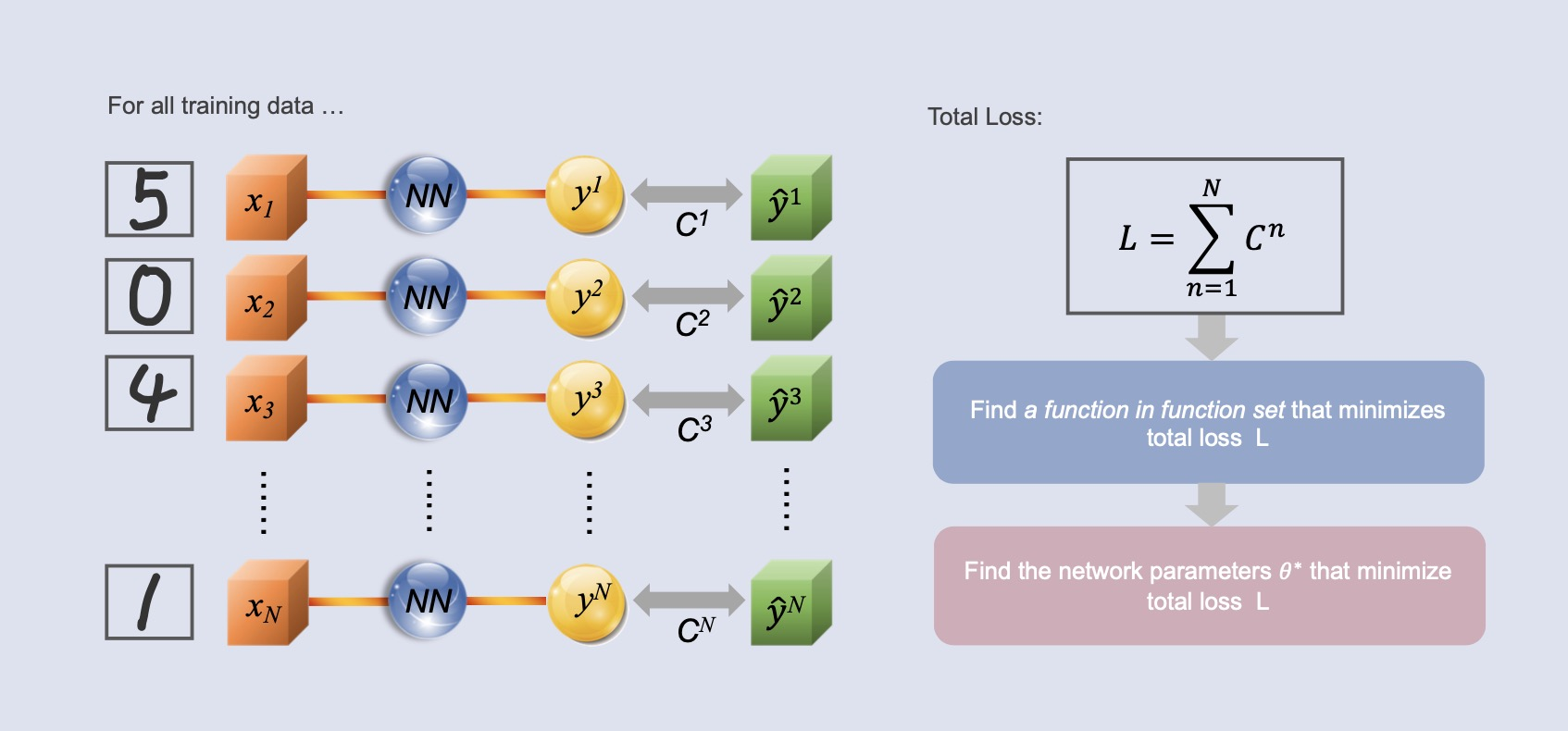
Minimizing Total Loss
When calculating loss, we don't just evaluate a single data point; instead, we assess the
overall loss across all training data. By summing the losses from each training instance, we
obtain a total loss LLL. The next step is to identify a set of functions within the function
set
that minimizes this total loss LLL, or to find a set of neural network parameters θ\thetaθ
that
achieves the same goal.
learn more
Finding Optimal
Functions and Parameters
Functions and Parameters
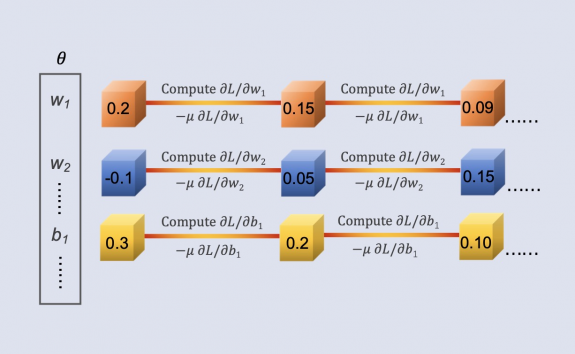
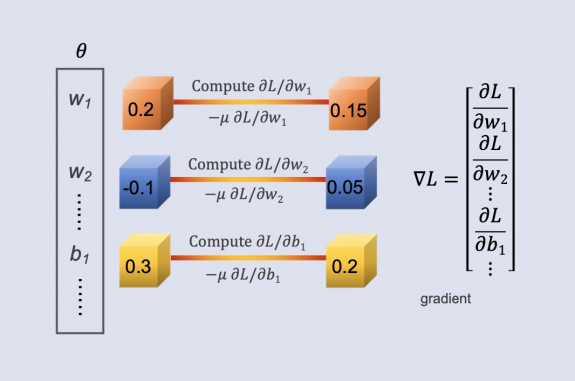


To find the optimal functions and the best set of parameters, we start by initializing θ with a
random value, which includes weights and biases. Next, we compute the partial derivatives of the
loss function for each parameter, resulting in a gradient vector denoted as ∇L. Using these
gradients, we then update the parameters to minimize the loss function, typically through
gradient
descent. This process is repeated iteratively, continuously recalculating gradients and refining
the
parameters, ultimately converging towards a set of parameters that minimizes the loss function
and
optimizes model performance.



